Priors bayesianas (1/3):¿Qué es una prior?

Imagina esto:
Estás buscando setas en un bosque. Nunca has estado allí, pero alguien te ha dicho que las mejores suelen crecer bajo robles. Aunque aún no has visto ninguna, ya sabes por dónde empezar a buscar. Eso que sabes antes de empezar a observar es tu conocimiento previo… o lo que en estadística bayesiana llamamos una distribución a priori, o simplemente: una prior.

¿Qué es una prior?

En el mundo de la inferencia bayesiana, una prior es nuestra forma de representar, con números, lo que creemos que puede pasar antes de ver los datos.

Es como una apuesta informada: antes de lanzar una moneda, quizás sospechas que está trucada porque el borde está desgastado. Eso afecta tu expectativa antes incluso de verla caer.

Cuando usamos el Teorema de Bayes, la prior se combina con los datos observados (a través de la verosimilitud) para actualizar nuestras creencias. El resultado es lo que llamamos la distribución posterior.

Como una imagen vale más que mil palabras a continuación ilustraremos con un gràfico este flujo de información “prior-verosimilitud-posterior”.

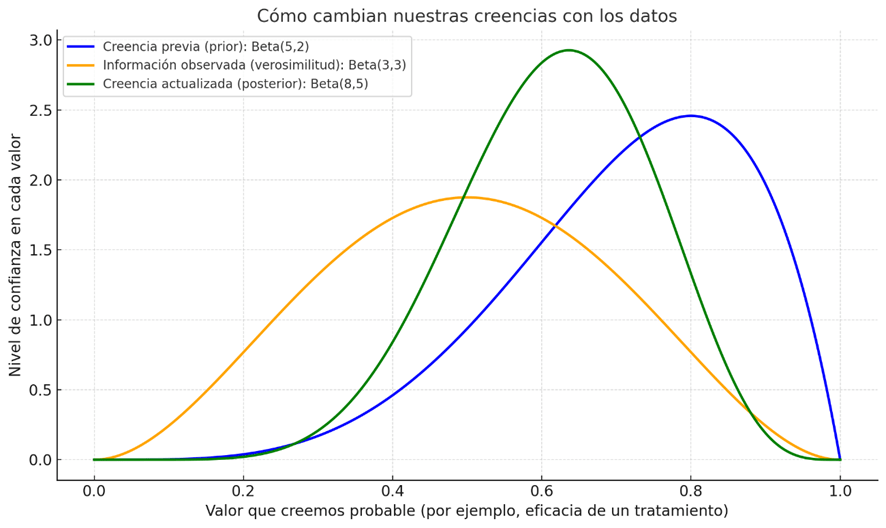
¿Qué muestra este gráfico?

• La prior (azul) refleja lo que creíamos antes de observar los datos.
• La verosimilitud (naranja) representa la información de los datos: más ancha y baja porque son pocos datos y aún hay mucha incertidumbre.
• La posterior (verde) es la combinación de ambas: una creencia más enfocada y precisa.

La altura de la curva indica cuánta confianza damos a cada valor. Una curva más alta y estrecha significa que estamos más seguros sobre un valor concreto. Cuando hay pocos datos, la prior influye más en el resultado final.

¿De dónde salen las priors?

Las creencias previas o priors se pueden clasificar según las siguientes características:

1. Cuánta información aportan
2. Qué propósito tienen
3. Cómo se comportan matemáticamente

Vamos una a una:

1. Según el grado de información que contienen

a) Prior informativa: expresa creencias claras y específicas basadas en datos previos, estudios anteriores o experiencia; se utiliza cuando ya sabemos bastante sobre el fenómeno que estamos modelando.

Ejemplo: Has observado que el 70 % de los pacientes con cierta medicación mejoran. Usas una prior que refleja esta experiencia.

b) Prior no informativa (o vaga): representa total ignorancia: asigna la misma probabilidad a todos los valores posibles y deja que sean los datos los que hablen.

Ejemplo: No sabes nada sobre el éxito de una nueva campaña. Usas una prior que asigna igual probabilidad a todos los valores posibles entre 0 y 1.

c) Prior débilmente informativa: introduce una estructura básica sin imponer creencias fuertes, útil cuando queremos evitar resultados extremos o inverosímiles sin condicionar demasiado el análisis.

Ejemplo: Sabes que una tasa de rotación de personal suele estar entre el 5 % y el 30 %, pero no quieres forzar demasiado la forma exacta. Usas una distribución que acote ese rango suavemente.

2. Según su propósito practico

a) Prior subjetiva: reflejan las creencias personales del analista o de un experto en la materia.

b) Prior empírica (o empíricamente informada): se construyen a partir de datos anteriores recogidos en contextos similares y pueden ser una forma sólida de incorporar conocimiento externo.

3. Según su forma matemática

a) Prior conjugada: se eligen porque, al combinarlas con la distribución de los datos mediante el teorema de Bayes, generan una distribución posterior del mismo tipo, lo que simplifica mucho los cálculos.

Ejemplo: Si los datos siguen una binomial (como lanzar una moneda), una prior beta es conjugada porque la posterior será también una beta.

b) Prior impropia: no son distribuciones de probabilidad válidas porque, por ejemplo, no se pueden normalizar; sin embargo, pueden utilizarse si aún así conducen a una posterior bien definida.

Ejemplo: Al no tener ninguna idea previa sobre el valor de una media, usamos una prior impropia constante: asumimos que todos los valores posibles, desde menos infinito hasta más infinito, son igualmente probables

¿Importa la elección de prior?

Muchísimo. Especialmente cuando tienes pocos datos:

• Con muchos datos, la prior influye poco: los datos tienen más peso.
• Con pocos datos, la prior puede inclinar el resultado final (la distribución posterior) de forma significativa.

Y no, una prior no es una manipulación. Todo lo contrario: es una forma transparente de mostrar tus creencias previas, y puedes justificarlas o compararlas con otras.

No obstante, no todas las priors tienen el mismo valor. ¿Que tipo de prior debemos aspirar a construir siempre que podamos? Obviamente una prior informativa, empírica y conjugada.

Para ello, nos debemos apoyar en tres estrategias complementarias:

1. Investigación cualitativa para intentar encontrar todas las posibles causas que expliquen el evento a predecir.
2. Análisis cuantitativo para reconocer patrones y predecir resultados futuros en función de los datos históricos.
3. Identificar la distribución de probabilidad del evento a predecir. En las próximas entregas de este blog veremos los grandes tipos de distribución que existen y que se clasifican en dos bloques: discretas y continuas.

En resumen

Una prior es nuestra brújula antes de tener datos.
Nos permite modelar la incertidumbre inicial y actualizarla con nueva información.

En estadística bayesiana, no empezamos desde cero: partimos de lo que ya sabemos (o creemos saber) y lo dejamos evolucionar con los datos.

¿Y ahora qué?

En la próxima entrada exploraremos cómo construir priors que sean conjugadas usando distribuciones discretas como la binomial o la Poisson, ideales para modelar conteos o eventos con resultados limitados. Porque, como veremos, ¡hasta nuestras suposiciones pueden tener forma matemática!