En las dos entradas anteriores presentamos el concepto de prior bayesiana y cómo construirla usando distribuciones discretas. Sin embargo, no todo en la vida se cuenta con números enteros. A veces, lo que queremos modelar fluye de forma continua: proporciones, medias, tiempos, tasas…
En este último capítulo de la serie, exploramos las distribuciones continuas más útiles para construir priors cuando las variables no se cuentan, sino que se miden.
¿Qué es una distribución continua?
Una distribución de probabilidad continua describe el comportamiento de una variable que puede tomar cualquier valor dentro de un intervalo, incluso infinitos valores posibles.
Por ejemplo: La proporción de pacientes que se recuperan de una enfermedad, el tiempo de espera en una consulta médica o el ingreso mensual medio de una familia.
Distribuciones continuas comunes para construir priors
1 – Distribución uniforme
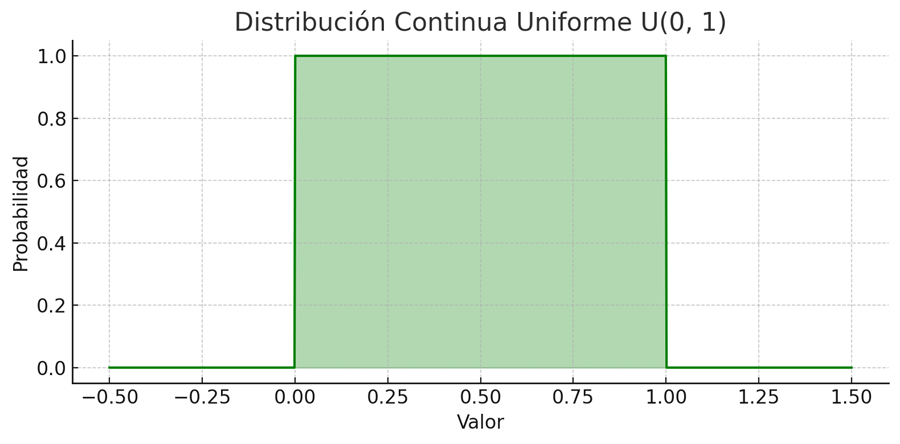
La distribución continua uniforme representa una situación en la que todas las posibilidades dentro de un intervalo tienen la misma probabilidad de ocurrir. Es el llamado “modelo de ignorancia total”.
La distribución continua uniforme representa una situación en la que todas las posibilidades dentro de un intervalo tienen la misma probabilidad de ocurrir. Es el llamado “modelo de ignorancia total”.
Ejemplo: si no tienes idea sobre el valor de una proporción entre 0 y 1, puedes usar una Uniforme(0, 1) como prior.
2 – Distribución normal (o gaussiana)
La distribución normal (o gaussiana) describe fenómenos donde los valores tienden a agruparse alrededor de una media, formando una curva en forma de campana: cuanto más lejos estás del centro, menos probable es observar ese valor.
Ejemplo: si esperas que el número medio de visitas diarias a un centro de salud sea 150 con una cierta variabilidad, puedes usar una Normal(μ=150, σ=20).

3 – Distribución beta
La distribución beta es una forma flexible de representar probabilidades entre 0 y 1, y se usa cuando queremos modelar nuestra incertidumbre sobre proporciones, como el porcentaje de éxito de un experimento, basándonos en observaciones previas.
La distribución beta es una forma flexible de representar probabilidades entre 0 y 1, y se usa cuando queremos modelar nuestra incertidumbre sobre proporciones, como el porcentaje de éxito de un experimento, basándonos en observaciones previas.
Ejemplo: crees que la eficacia de una vacuna está alrededor del 80 %, pero podría variar ligeramente. Una Beta(8, 2) puede reflejar esa creencia.

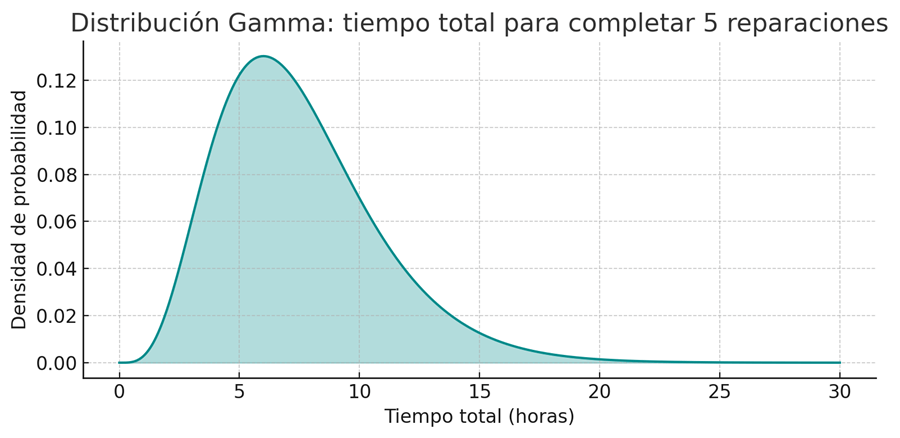
4 – Distribución gamma
La distribución gamma se usa para modelar tiempos hasta que ocurre un evento, especialmente cuando ese evento resulta de la acumulación de varios sucesos más pequeños.
Ejemplo: El tiempo total que tarda un técnico en completar 5 reparaciones consecutivas, si cada una lleva un tiempo promedio de 1,5 horas, se puede modelar con una distribución gamma.
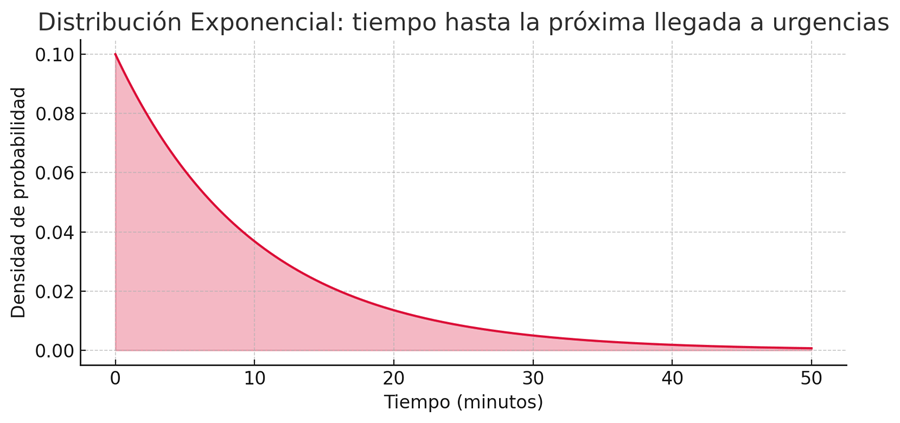
5 – Distribución exponencial
La distribución exponencial modela el tiempo que transcurre hasta que ocurre un único evento aleatorio, como la llegada de un paciente a urgencias o la avería de una máquina, cuando estos eventos ocurren de forma constante e independiente en el tiempo. Es una distribución solo para valores positivos y con una caída rápida: eventos más lejanos en el tiempo son menos probables.
Ejemplo: El tiempo que puede pasar hasta que llegue el próximo paciente a urgencias, si en promedio llega uno cada 10 minutos.
¿Por qué usar estas distribuciones como priors?
Las distribuciones continuas permiten:
- Representar creencias con precisión cuando las variables no se pueden contar, sino que se miden.
- Ajustar la forma de la curva según la certeza o incertidumbre previa
- Usar distribuciones conjugadas que simplifican los cálculos matemáticos.
Ejemplo visual: cómo modelar creencias con la distribución Beta
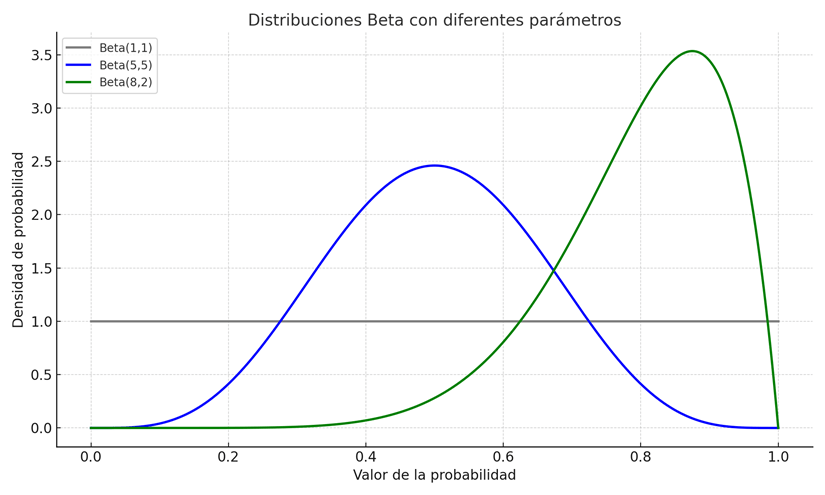
¿Qué muestra este gráfico?
Representa tres distribuciones Beta distintas, cada una expresando una creencia diferente sobre una probabilidad entre 0 y 1.
- Beta(1,1): en gris, representa total incertidumbre; todos los valores de probabilidad son igualmente posibles. Muy similar a la distribución uniforme
- Beta(5,5): en azul, representa una creencia moderada de que la probabilidad está en torno a 0,5. Muy similar a la distribución normal
- Beta(8,2): en verde, refleja una creencia informada de que la probabilidad es alta (cerca de 0,8).
Este tipo de visualización permite ver cómo los parámetros de la distribución Beta ayudan a ajustar la forma de la prior según la información previa disponible. Vale la pena fijarse en que en función del valor de estos parámetros se pueden representar otras distribuciones antes descritas (p.e. la uniforme o la normal). Esto demuestra la flexibilidad de la distribución Beta.
Conclusión
Las distribuciones continuas son esenciales en la construcción de priors bayesianas cuando el fenómeno que se quiere modelar no se puede reducir a contar eventos. Son flexibles, ajustables y permiten incorporar conocimiento experto de forma precisa y transparente.
La elección de una buena prior continua no es un acto de fe, sino una herramienta rigurosa que enriquece los modelos estadísticos y los conecta con el mundo real.
Con esta tercera entrada finaliza la serie introductoria sobre priors bayesianas. A partir de aquí, el lector ya tiene una base sólida para entender cómo expresar creencias previas y cómo esas creencias evolucionan con los datos. En futuras publicaciones abordaremos cómo elegir una prior en situaciones reales, cómo validar su impacto y cómo usarlas en modelos complejos.

