En la primera entrega de esta serie vimos qué es una prior: una forma de expresar con números lo que creemos antes de observar datos. Hoy daremos un paso más y veremos cómo podemos construir esas priors utilizando distribuciones de probabilidad discretas cuando el análisis preliminar nos indica que el fenómeno que queremos predecir se comporta así.
Porque sí, hasta nuestras corazonadas pueden adoptar una forma matemática.
¿Qué es una distribución de probabilidad discreta?
Una distribución de probabilidad discreta es una herramienta matemática que asigna probabilidades a valores enteros concretos. Es útil para describir fenómenos contables como:
- ¿Cuántas veces encestaré si lanzo 10 veces?
- ¿Cuántos clientes vendrán hoy?
- ¿Cuánto tardaré en tener un acierto?
Estas distribuciones no trabajan con valores continuos como 3,1416 o 7,82, sino con 0, 1, 2, 3…
Las distribuciones discretas más útiles para construir priors
1 – Bernoulli
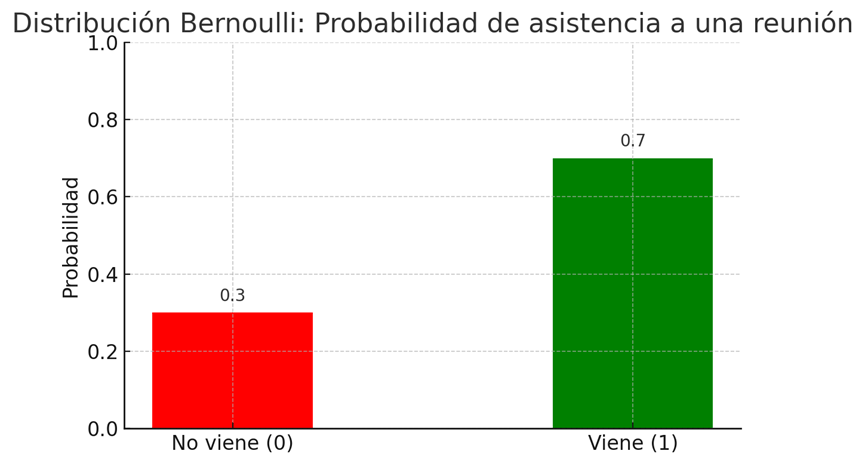
La distribución de Bernoulli describe la probabilidad de experimentos con solo dos posibles resultados, como lanzar una moneda y obtener cara o cruz. Es el modelo más simple porquè sólo tiene dos variables: éxito o fracaso (1 o 0).
Ejemplo de prior: ¿Crees que hay un 70 % de probabilidad de que alguien acuda a una reunión? Puedes expresar esa creencia con una distribución Bernoulli.
2 – Binomial
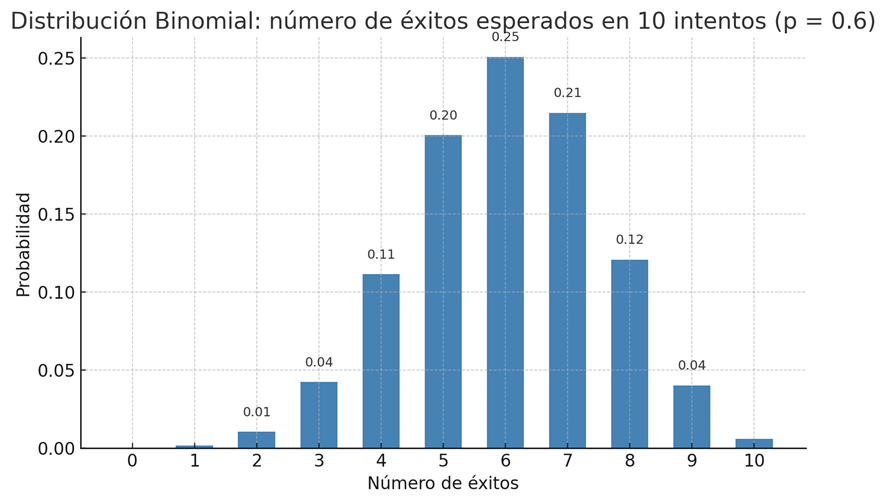
La distribución binomial describe el número de éxitos en un número fijo de intentos, cuando cada intento tiene solo dos posibles resultados y la misma probabilidad de éxito. Es muy útil cuando tienes alguna información previa sobre tasas de éxito.
Ejemplo: si crees que un producto tiene un 60 % de éxito y lo probarás 10 veces, una prior binomial puede representar cuántos éxitos esperas.
3 – Geométrica
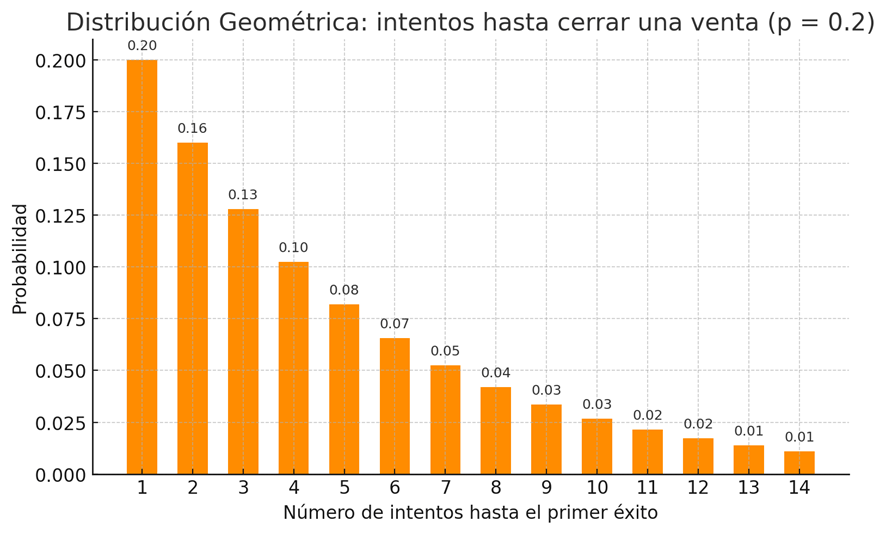
La distribución geométrica describe cuántos intentos se necesitan hasta obtener el primer éxito en una serie de pruebas con dos posibles resultados y probabilidad constante.
Ejemplo de prior: estimar cuántos intentos harán falta para cerrar una venta si el éxito en cada llamada es del 20 %.
4 – De Poisson
La distribución de Poisson describe cuántas veces ocurre un evento en un intervalo de tiempo o espacio fijo, cuando los eventos son raros pero suceden a una tasa promedio constante.
Ejemplo de prior: crees que en promedio hay 3 errores al día en un sistema informático. Usas una Poisson (λ = 3) como prior para predecir cuántos errores esperar hoy.
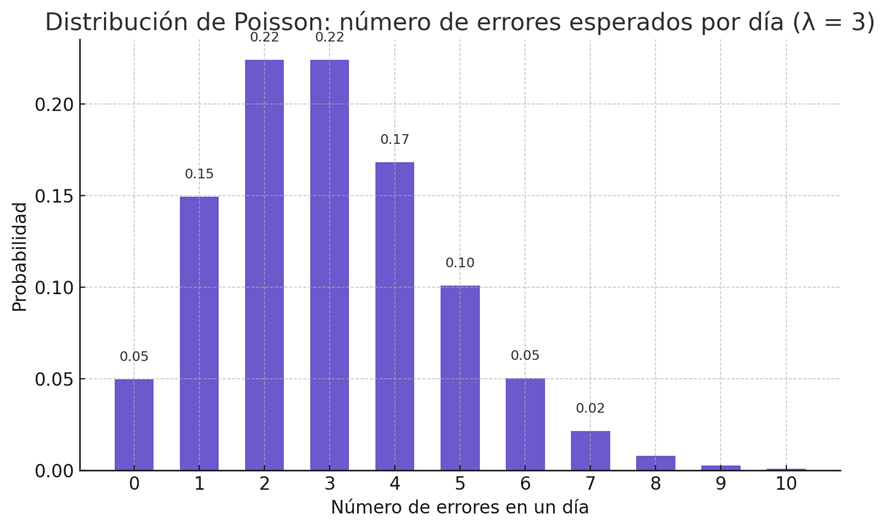
¿Cómo se usan como priors?
Estas distribuciones permiten construir priors que:
- Sean coherentes con tu conocimiento previo.
- Sean fáciles de combinar con datos reales.
- Sean conjugadas, es decir, que faciliten el cálculo de la posterior (por ejemplo: la prior binomial con verosimilitud binomial).
No se trata de usar estas distribuciones al azar, sino de elegir la que encaje con el tipo de dato que se modela (conteo, proporción, repeticiones…) y con lo que ya se sabe.
Ejemplo visual: cómo se comporta la distribución binomial
A continuación se muestra un gráfico comparativo de la distribución binomial para 10 intentos, con tres valores distintos de probabilidad de éxito (p = 0.2, 0.5 y 0.8):
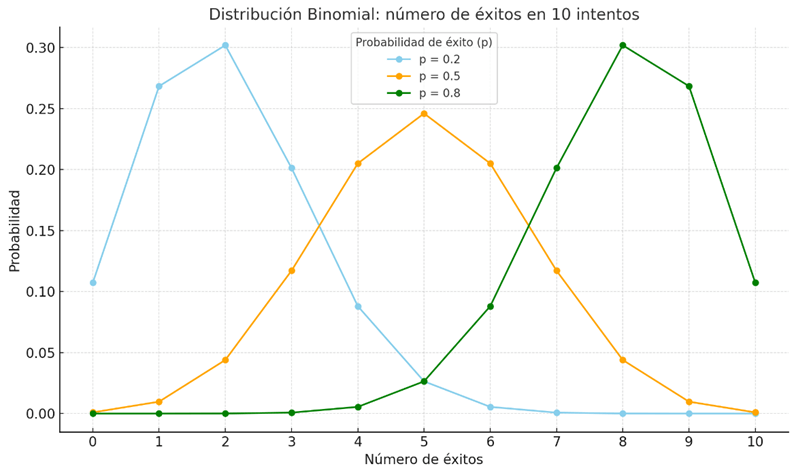
¿Qué muestra este gráfico?
Representa la probabilidad de obtener entre 0 y 10 éxitos al realizar 10 intentos (por ejemplo, lanzar un dado o probar un tratamiento) para distintos niveles de probabilidad de éxito p.
- En azul (p = 0.2): la mayoría de los resultados probables están en el extremo izquierdo (pocos éxitos), porque se espera fallar más que acertar.
- En naranja (p = 0.5): la distribución es simétrica, con más peso en 5 éxitos, lo que indica incertidumbre balanceada.
- En verde (p = 0.8): la masa de probabilidad se desplaza hacia la derecha, reflejando una expectativa alta de éxito.
Este gráfico ilustra cómo una distribución binomial puede reflejar distintas creencias a priori sobre el número de éxitos esperados antes de ver los datos reales.
Conclusión
Las distribuciones discretas son herramientas precisas y versátiles para construir priors cuando:
- Los resultados posibles son enteros o eventos contables.
- Ya se dispone de alguna idea o experiencia previa.
- Se buscan modelos simples pero potentes.
No es magia, es modelado: expresar ideas sobre el mundo con números antes de ver lo que pasa.
¿Y ahora qué?
En la tercera y última entrada de la serie veremos cómo usar distribuciones continuas como la Normal o la Beta para construir priors cuando nuestras creencias no se pueden contar, sino que fluyen.